কোলমোগোরভের বিপুল অবদান

প্রখ্যাত গণিতবিদ আন্দ্রেই কোলমোগোরভ (২৫/৪/১৯০৩- ২০/১০/১৯৮৭)। রাশিয়ার তাম্বোভে জন্মগ্রহণ করেন। সম্ভাব্যতা তত্ত্ব, রাশিবিজ্ঞান এবং অশান্ত প্রবাহ – বিষয়গুলির ক্ষেত্রে তিনি এক অন্যতম প্রধান ব্যক্তিত্ব। গণিতের বিভিন্ন শাখায়, তার বিশাল অবদান এবং যুগান্তকারী আবিষ্কারগুলি বৈপ্লবিক পরিবর্তন এনে দেয়। আজ আমরা যেভাবে সম্ভাবনাভিত্তিক প্রক্রিয়া (random processes) এবং ফ্লুইড মেকানিক্সকে বুঝি তাতে, ওনার অবদান, বিরাট মাপের।

অশান্ত প্রবাহ

ফ্লুইড মেকানিক্সে, অশান্ত প্রবাহকে বোঝার ক্ষেত্রে আন্দ্রেই এর অবদান অত্যন্ত গুরুত্বপূর্ণ। অশান্ততার ধারণায়, বিভিন্ন দৈর্ঘ্যের স্কেল জুড়ে এডিসমূহের (ঘূর্ণিপাক) স্ব-অনুরূপ ক্যাসকেডের উদ্ভাবক তিনিই। যুগান্তকারী এই তত্ত্ব, ‘কলমোগোরভের অশান্ততা তত্ত্ব’ ( Turbulence Theory) নামে পরিচিত। অশান্ত ফ্লুইডের আচরণ সম্পর্কে তিনি গুরুত্বপূর্ণ অন্তর্দৃষ্টি রাখেন। অশান্ততা অধ্যয়নের ক্ষেত্রে একটি মৌলিক কাঠামো – এই তত্ত্ব। তিনি সমীকরণের একটি সেট তৈরি করেন যা ‘কোলমোগোরভ সমীকরণ’ নামে পরিচিত। সমীকরণগুলি, অশান্ততার পরিসংখ্যানগত বৈশিষ্ট্যসমূহের বর্ণনা দেয় । এমনকি অশান্ততার আচরণ বিশ্লেষণ এবং ভবিষ্যদ্বাণী করার জন্যও সন্ধান দেয়। অশান্ততা সম্পর্কে তাঁর গভীর উপলব্ধি আবহাওয়াবিদ্যা, প্রযুক্তি এমনকি জটিল পদ্ধতি অধ্যয়নের ক্ষেত্রে সুদূরপ্রসারী প্রভাব ফেলেছে। শুধু তত্ত্ব কথায় নয় ! বরং বাস্তব পরিস্থিতিতে, অশান্তপ্রবাহ অধ্যয়ন করার জন্য তিনি উদ্ভাবনী কৌশল ব্যবহার করে ব্যাপক পরীক্ষামূলক গবেষণা পরিচালনা করেন। তাঁর পরীক্ষাগুলি কেবল যে তাঁর তাত্ত্বিক কাঠামোকেই বৈধতা দিয়েছে তা নয়, উপরন্তু অশান্ত প্রবাহের মডেলগুলিকে আরও বিশ্লেষণের মধ্যে দিয়ে গিয়ে তা পরিমার্জনের জন্য মূল্যবান তথ্য সরবরাহ করেছে।

ফ্লুইড পদ্ধতি পরিকল্পনায় , তাপ স্থানান্তর বা ভর স্থানান্তর, বিচ্ছুরণ, মিশ্রণ এবং অনুরূপ প্রয়োগগুলিতে এই অশান্ত প্রবাহ একটি গুরুত্বপূর্ণ ভূমিকা পালন করে। যেমন, ‘টার্বুলেন্স’ বা দ্ব্যর্থতা নিরসন মডেলিং এবং বিশ্লেষণ একটি কঠিন বিষয়। এটি, প্রবাহের সময়, প্রবর্তিত এডিস (ঘূর্ণিপাক) এবং গতিশক্তির কারণে ঘটে, যা প্রবাহের বৈশিষ্ট্যগুলির ভবিষ্যদ্বাণীকে সমস্যাসংকুল করে তোলে। অশান্ত গতিশক্তি একটি যান্ত্রিক প্রণালীতে তাদের আচরণগুলিকে সংজ্ঞায়িত করার প্রয়াস করে। এক্ষেত্রে ভিন্ন প্রবাহের কারণগুলির পরিসংখ্যানগত বিশ্লেষণকে নিশ্চিত করে। বাহ্যিক কিংবা অভ্যন্তরীণ প্রবাহ ব্যবস্থায় অশান্ত গতিশক্তি গণনা, বেশিরভাগ ক্ষেত্রেই কম্পিউটেশনাল ফ্লুইড ডাইন্যামিক্‌স-এর (CFD) ওপর নির্ভরশীল। বিভিন্ন প্রবাহ এবং সীমান্তবর্তী অবস্থার জন্য শক্তি এবং অপচয় হারের সঠিক গণনার মাধ্যমে, জটিল অশান্ত প্রবাহ সিস্টেমের সুনির্দিষ্ট CFD মডেলিং নিশ্চিত করা হয়। প্রসঙ্গত CFD হল ফ্লুইড মেকানিক্সের একটি শাখা যা ফ্লুইড প্রবাহ অনুকরণ এবং বিশ্লেষণ করতে কম্পিউটার ব্যবহার করে। এতে ফ্লুইড প্রবাহ সম্পর্কিত সমস্যা সমাধানের জন্য সংখ্যাসূচক বিশ্লেষণ এবং ডেটা স্ট্রাকচার ব্যবহার করা হয় । তরল আর গ্যাসগুলি কীভাবে পৃষ্ঠতলের সাথে যোগাযোগ করে, অপরদিকে একটি নির্দিষ্ট স্থানের মধ্য দিয়ে কিভাবে প্রবাহিত হয় তা অনুমান করতে সহায়তা করে এই CFD। ব্যবহারিক জীবনে ফ্লুইড প্রবাহ বিশ্লেষণের কাজে এটিকে ব্যবহার করা যেতে পারে। উদাহরণ স্বরূপ পাখির ওড়া কিংবা ধমনীতে ইঞ্জেকশন দেওয়ার বিষয়গুলিকেই দেখা যায়।

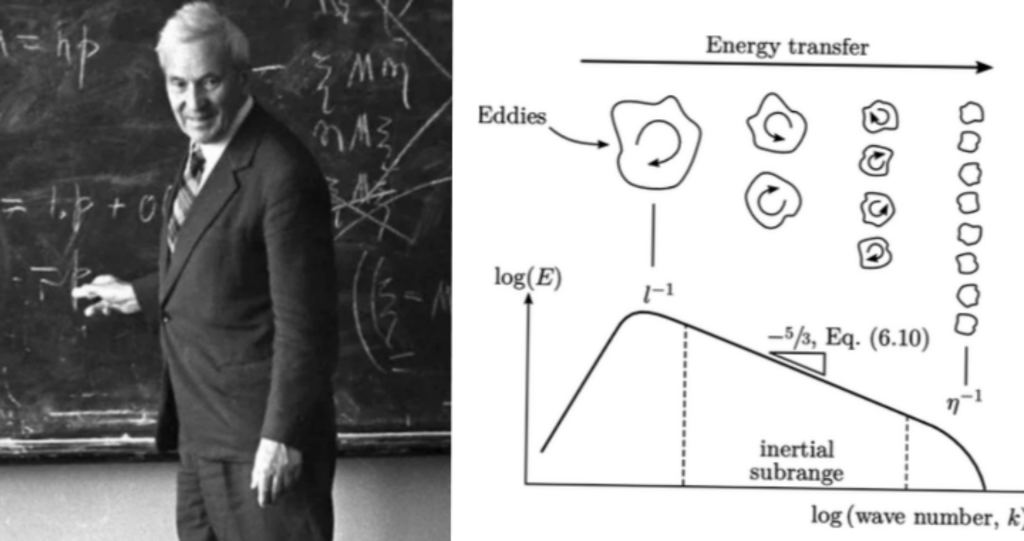
অশান্ত প্রবাহ বিভিন্ন আকারের অশান্ত ঘূর্ণিপাক (এডি) দ্বারা গঠিত। উচ্চ রেনল্ডস সংখ্যায়, বৃহত্তম এডি এবং ক্ষুদ্রতম এডিগুলির মধ্যে একটি স্কেল ব্যবধান বিদ্যমান। বৃহত্তম এডিগুলি শক্তি উৎপাদন হিসাবে গড় প্রবাহ থেকে গতিশক্তি আহরণ করে। এক্ষেত্রে, দৈর্ঘ্যের স্কেল প্রবাহের মাত্রার সাথে তুলনীয়। এই প্রক্রিয়াগুলি অত্যন্ত অ্যানিসোট্রপিক, অর্থাৎ এর ভৌত বৈশিষ্ট্য এমন যে বিভিন্ন দিকে পরিমাপ করার সময় ভিন্ন ভিন্ন মান পাওয়া যায়। এর বেশিরভাগই সান্দ্রতা দ্বারা প্রভাবিত হয় না। বেশিরভাগ পরিবহন এবং মিশ্রণ একই পরিসরেই ঘটে। অপরদিকে ক্ষুদ্রতম এডির রয়েছে সর্বজনীন বৈশিষ্ট্য। এর প্রবাহ জ্যামিতি এবং অবস্থার সাপেক্ষে স্বাধীন। এই পরিসরে থাকা এডিগুলি সাধারণত বড় এডি থেকে শক্তি সংগ্রহ করে। তরলের আণবিক সান্দ্রতার মাধ্যমে এগুলি নিজের শক্তিকে তাপের মধ্যে ছড়িয়ে দেয়। এই এডিগুলি কোলমোগোরভ স্কেল দ্বারা বর্ণিত। যা দৈর্ঘ্যের স্কেল সহ আইসোট্রপিক । যার অর্থ এটির ভৌত বৈশিষ্ট্য এমন যে বিভিন্ন দিকে পরিমাপ করার সময় এর একই মান দেখায়। অনুমান করা হয়, ক্ষুদ্রাকার এডিগুলি সান্দ্রতা এবং অপসারণ দ্বারা নির্ধারিত হয়। এটির শক্তি বর্ণালীর বিচ্ছিন্ন পরিসরের মধ্যে থাকে। বিচ্ছুরণযোগ্য সীমার মধ্যে অশান্ত প্রান্তগুলি আইসোট্রোপিক হয় । এর কারণ শক্তিশালী সান্দ্রতার বিচ্ছুরণমূলক ক্রিয়াগুলি ,বৃহত্তর প্রান্তগুলির অ্যানিসোট্রপিক বৈশিষ্ট্যগুলিকে বহিষ্কার করে দেয়। এই অঞ্চলে বৃহত্তর এডি থেকে প্রাপ্ত গতিশক্তি তাপে ছড়িয়ে পড়ে। এই অঞ্চলের দৈর্ঘ্যের স্কেলটিকে কিনেমেটিক (সৃতিবিদ্যা-সম্মত) সান্দ্রতার একটি ফাংশন বলে ধরে নেওয়া হয়। এই অঞ্চলে বৃহত্তর এডি থেকে প্রাপ্ত গতিশক্তি তাপে ছড়িয়ে পড়ে।

এই ব্যাখ্যার মাধ্যমে আমরা চারটি গুরুত্বপূর্ণ ধারণা পাই : ১) কলমোগোরভ দৈর্ঘ্যের স্কেল ; ২) কলমোগোরভ টাইম স্কেল ; ৩) কলমোগোরভ বেগ স্কেল ৪) শক্তি বর্ণালী ।

তাত্ত্বিক অবদানের পাশাপাশি কলমোগোরভ পরীক্ষামূলক ফ্লুইড গতিবিদ্যাতেও উল্লেখযোগ্য অগ্রগতি করেছিলেন। তিনি ফ্লুইড প্রবাহের অন্তর্নিহিত প্রক্রিয়াগুলি সম্পর্কে মূল্যবান অন্তর্দৃষ্টি দেন। বিভিন্ন পরিস্থিতিতে ফ্লুইডের আচরণ অধ্যয়ন করার জন্য অসংখ্য পরীক্ষা-নিরীক্ষা পরিচালনা করেন। তার অগ্রগামী কাজ এবং উদ্ভাবনী ধারণাগুলি এই শাখাগুলিকে শুধুমাত্র উন্নতই করেনি, তার সাথে বিশ্বব্যাপী গণিতবিদ এবং বিজ্ঞানীদের একাধিক প্রজন্মকে অনুপ্রাণিত করেছে। এইসব অবদানের মাধ্যমে, কলমোগোরভ এক স্থায়ী উত্তরাধিকার রেখে গেছেন। কলমোগোরভের কাজ স্টোকাস্টিক (সম্ভাবনা-ভিত্তিক) ডিফারেনশিয়াল সমীকরণের ভিত্তি স্থাপন করে। পদার্থবিদ্যা, জীববিজ্ঞান এবং অর্থনীতির বিভিন্ন ঘটনার মডেলিং এবং বিশ্লেষণের অবিচ্ছেদ্য অঙ্গ হয়ে উঠেছে, এই সমীকরণ। স্টোকাস্টিক ডিফারেনশিয়াল সমীকরণগুলি গাণিতিক মডেলগুলিতে সম্ভাবনাভিত্তিক (random) ওঠানামাগুলিকে অন্তর্ভুক্ত করার সুযোগ করে দিয়ে বাস্তব পরিস্থিতি আবার বাস্তবসম্মত পূর্বাভাস দানের ক্ষমতা বাড়িয়ে দিয়েছেন কলমোগোরভ।