পর্ব – ৩
১২ আগস্ট ১৯০৪-এ জার্মানির হাইডেলবার্গে গণিতবিদদের তৃতীয় আন্তর্জাতিক কংগ্রেসে উপস্থাপিত একটি গবেষণাপত্রে লুডভিগ প্রান্ড্টল (Ludwig Prandtl, ১৮৭৫-১৯৫৩) বায়ুগত সীমানা স্তরের(Boundary Layer) ধারণাটি প্রথম উত্থাপন করেন। এখানে একটু বলে রাখা দরকার আমরা যেকোনো ধরনের বলবিদ্যায় ভর, ভরবেগ ও শক্তির সংরক্ষণ নিয়ে কথা বলে থাকি। তরল বলবিদ্যায় ভরবেগ ও শক্তির সংরক্ষণের ক্ষেত্রে Navier-Stokes সমীকরণ হল সবচেয়ে গুরুত্বপূর্ণ সমীকরণ। এই সমীকরণের সম্পূর্ণ সমাধান আজও অবধি পাওয়া যায় নি, কিছু বিশেষ ক্ষেত্র ছাড়া। প্র্যান্ডটল্-এর এই গবেষণার ফলস্বরূপ বেরিয়ে আসে একটি নতুন তত্ত্ব যার নাম Boundary Layer Theory। এই তত্ত্বের মাধ্যমে আমরা Navier-Stokes সমীকরণের অনেক সন্নিকটবর্তী (approximated) সমাধান দিতে পারি। এতদিন তরল বলবিদ্যা ছিল গণিতবিদদের মূল চর্চার বিষয়; এবার তা পদার্থবিজ্ঞানী ও ইঞ্জিনিয়ারদেরও গবেষণার এক চমৎকার জায়গা হয়ে উঠল। (দ্রষ্টব্য https://bigyanbhash.org/%e0%a6%93%e0%a6%b2%e0%a6%97%e0%a6%be-%e0%a6%b2%e0%a7%87%e0%a6%a1%e0%a6%bf%e0%a6%9c%e0%a7%87%e0%a6%a8%e0%a6%b8%e0%a7%8d%e0%a6%95%e0%a6%be%e0%a6%af%e0%a6%bc%e0%a6%be-%e0%a6%93-%e0%a6%a8%e0%a7%8d/)
এবার বুঝে নেওয়া যাক এর গুরুত্ব। এটি প্রবাহ ক্ষেত্রটিকে দুটি এলাকায় বিভক্ত করে তরল প্রবাহের সমীকরণকে সরল করে তোলে: একটি সীমানা স্তরের ভিতরে। এটি সান্দ্রতা দ্বারা প্রভাবিত। এখানে সীমানা স্তরে থাকা বস্তু বেশিরভাগ টান অনুভব করে। অপরটি সীমানা স্তরের বাইরে। এটি সান্দ্রতাকে উপেক্ষা করা যায়, কারণ তা সমাধানের উপর উল্লেখযোগ্য প্রভাব ফেলে না। এটি সম্পূর্ণ নেভিয়ার-স্টোকস সমীকরণের সরলীকরণ করে উভয় ক্ষেত্রেই প্রবাহের জন্য একটি বদ্ধ-প্রকারের (closed-form) সমাধানের সুযোগ করে দেয় । একই অনুমান অন্যান্য ফ্লুইড (বাতাস ছাড়াও) সম্পর্কে প্রযোজ্য, যার সান্দ্রতা মাঝারি থেকে কম.- যেমন জল। যে ক্ষেত্রে পৃষ্ঠ এবং ‘বাল্ক ফ্লুইডে’র মধ্যে তাপমাত্রার পার্থক্য থাকে, সেখানে দেখা যায় যে একটি দেহ থেকে তাপ স্থানান্তরের বেশিরভাগই বেগের সীমানা স্তরের আশেপাশে সঞ্চালিত হয়। এটি আবার সীমানা স্তরের বাইরে প্রবাহ ক্ষেত্রের সমীকরণগুলিকে সরল করার সুযোগ করে দেয়। সীমানা স্তর জুড়ে চাপ বন্টন পৃষ্ঠের স্বাভাবিক দিকের দিকে (যেমন একটি এয়ারফয়েল ) সীমানা স্তর জুড়ে তুলনামূলকভাবে স্থির থাকে।
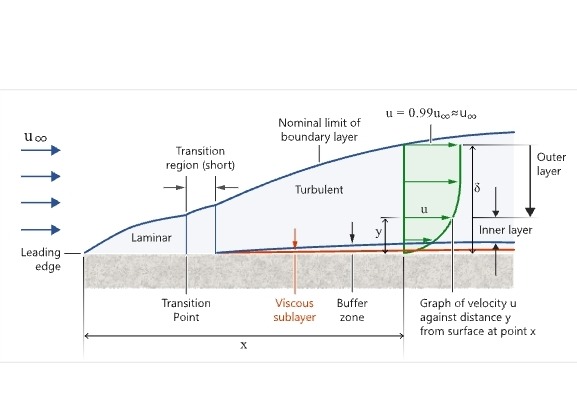
পুরুত্বকে সাধারণত কঠিন দেহ থেকে বিন্দু পর্যন্ত দূরত্ব হিসাবে সংজ্ঞায়িত করা হয়, যেখানে সান্দ্র প্রবাহের (viscous flow) বেগ মুক্তধারার বেগ (freeflow) (একটি অদৃশ্য প্রবাহের পৃষ্ঠের বেগ) এর 99% । ‘স্থানচ্যুতি পুরুত্ব’ হল একটি বিকল্প সংজ্ঞা যেখানে বলা হয়েছে যে সীমানা স্তরটি প্রাচীরের স্লিপ সহ অদৃশ্য প্রবাহের তুলনায় ভর প্রবাহের ঘাটতির প্রতিনিধিত্ব করে। এটি হল সেই দূরত্ব যার দ্বারা প্রাচীরটিকে অদৃশ্য ক্ষেত্রে স্থানচ্যুত করতে হবে যাতে সান্দ্র ক্ষেত্রের মতো একই মোট ভর প্রবাহ দেওয়া হয়। ‘নো-স্লিপ’ অবস্থার জন্য কঠিন বস্তুর পৃষ্ঠে প্রবাহের বেগ শূন্য এবং তরল তাপমাত্রা পৃষ্ঠের তাপমাত্রার সমান হওয়া প্রয়োজন। প্রবাহ বেগ তারপর সীমানা স্তরের মধ্যে দ্রুত বৃদ্ধি পাবে, নীচের সীমানা স্তর সমীকরণ দ্বারা নিয়ন্ত্রিত।
একইভাবে তাপীয় সীমানা স্তর (Thermal Boundary Layer) হল কঠিন দেহ থেকে দূরত্ব যেখানে তাপমাত্রা মুক্ত প্রবাহ (ফ্রি স্ট্রিম) যা তাপমাত্রার 99%। দুটি পুরুত্বের অনুপাত Prandtl সংখ্যা দ্বারা নিয়ন্ত্রিত হয় ।
গ্লাইডার, বণিজ্যিক বিমান প্রভৃতি উচ্চ কর্মশীলতার ডিজাইনে সীমানা স্তরের আচরণ নিয়ন্ত্রণ করে বিমানের ড্র্যাগ কমিয়ে ন্যূনতম মাত্রায় নিয়ে আসার দিকে বিশেষ নজর দেওয়া হয়। চলমান বস্তুর পৃষ্ঠতল আর ফ্লুইডের ঘর্ষণ জনিত যে-প্রতিরোধ বল বস্তুটির উপর ক্রিয়া করে তাকে বলে ‘ঘর্ষণ ড্র্যাগ’ কিংবা ‘ত্বক ড্র্যাগ’। বিমানের ক্ষেত্রে দুটো ক্রিয়ার দিকে খেয়াল রাখতে হয়। এক, সীমানা স্তর স্থানচ্যুতি জনিত বেধ বা পুরুত্বের জন্য বিমানের দেহর কার্যকর বেধ বা পুরুত্ব বাড়িয়ে তোলে। তার ফলে চাপজনিত ড্র্যাগ বেড়ে যায়। দুই, বিমানের ডানার পৃষ্ঠতলের পিড়ন জনিত বিকৃতি বা ‘শিয়ার’ বল ত্বক ঘর্ষণ জনিত ড্র্যাগ সৃষ্টি করে।
পাইপের মধ্য দিয়ে ফ্লুইড প্রবাহর ধরণ নির্ণয় করবার জন্য ‘রেনল্ড্ সংখ্যা’ নামক একটি অনুপাত ব্যবহার করা হয়। উচ্চ রেনল্ড সংখ্যার (High Reynolds Number) প্রবাহ পূর্ণ-আকারের বিমানের ক্ষেত্রে প্রযোজ্য। এখানে একটি লেমিনার সীমানা স্তর থাকা বাঞ্ছনীয় । লেমিনার প্রবাহের নিজস্ব বেগ-বৈশিষ্ট্যের কারণে এটি একটি নিম্ন ত্বকের ঘর্ষণে পরিণত হয়। যার কারণে সীমানা স্তরটি অনিবার্যভাবে ঘন হয়ে যায় এবং কম স্থিতিশীল হয়ে ওঠে । বিমানের দেহের সাথে প্রবাহটি বিকাশ লাভ করে এবং শেষ পর্যন্ত টারবুলেন্ট হয়ে ওঠে ।
নিম্ন রেনল্ডস সংখ্যার প্রবাহ মডেলে লেমিনার প্রবাহ বজায় রাখা তুলনামূলকভাবে সহজ। এটি কম ত্বকের ঘর্ষণ দেয়, যা কাম্য। যাইহোক, একই বেগ –বৈশিষ্ট্য যা ল্যামিনার সীমানা স্তরকে তার কম ত্বকের ঘর্ষণ দেয় সেটি প্রতিকূল চাপ গ্রেডিয়েন্ট দ্বারা খারাপভাবে প্রভাবিত হয়। বিমানের উইং কর্ডের পিছনের অংশের উপর চাপ পুনরুদ্ধার শুরু হলে, একটি ল্যামিনার সীমানা স্তর পৃষ্ঠ থেকে আলাদা হতে থাকে। এই ধরনের প্রবাহ বিচ্ছেদ চাপ টেনে একটি বড় বৃদ্ধি ঘটায় , যেহেতু এটি উইং বিভাগের কার্যকরী আকারকে ব্যাপকভাবে বাড়িয়ে দেয়। এই ক্ষেত্রে, একটি টার্বুলেটার ব্যবহার করে, ল্যামিনার বিচ্ছেদের অবস্থানের আগে একটি বিন্দুতে ইচ্ছাকৃতভাবে সীমানা স্তরটিকে অশান্ত অবস্থায় নিয়ে যাওয়া সুবিধাজনক হতে পারে । অশান্ত সীমানা স্তরের পূর্ণ বেগ বৈশিষ্ট্য এটিকে বিচ্ছিন্ন না করে প্রতিকূল চাপ গ্রেডিয়েন্ট বজায় রাখতে দেয়। এইভাবে, ত্বকের ঘর্ষণ বৃদ্ধি পেলেও সামগ্রিকভাবে টানাটানি কমে যায়। গল্ফ বলের ‘ডিম্পলিং’, বিমানের ঘূর্ণি জেনারেটর প্রভৃতির পিছনেও এই নীতি কাজ করে । বিশেষ উইং বিভাগগুলিও ডিজাইন করা হয়েছে চাপ পুনরুদ্ধারের উপযোগী করে, যাতে ল্যামিনার বিচ্ছেদ হ্রাস পায় বা এটি নির্মূল হয়।
সীমানা স্তর সমীকরণের আবির্ভাব ছিল তরল গতিবিদ্যার সবচেয়ে গুরুত্বপূর্ণ অগ্রগতিগুলির মধ্যে একটি। মাত্রা বিশ্লেষণের একটি ক্রম ব্যবহার করে, সান্দ্র তরল প্রবাহের সুপরিচিত গভর্নিং নেভিয়ার-স্টোকস সমীকরণগুলি সীমানা স্তরের মধ্যে ব্যাপকভাবে সরল করা যেতে পারে। উল্লেখযোগ্যভাবে, আংশিক ডিফারেনশিয়াল ইকুয়েশন (PDE) এর বৈশিষ্ট্য সম্পূর্ণ নেভিয়ার-স্টোকস সমীকরণের উপবৃত্তাকার রূপের পরিবর্তে প্যারাবোলিক হয়ে ওঠে। এটি সমীকরণের সমাধানকে ব্যাপকভাবে সরল করে। সীমানা স্তরের আনুমানিকতা তৈরি করে, প্রবাহটিকে একটি অদৃশ্য অংশে (যা বেশ কয়েকটি পদ্ধতি দ্বারা সমাধান করা সহজ) এবং সীমানা স্তরে বিভক্ত করা হয়। এখানে কিছু গাণিতিক রূপান্তর (transformation) ব্যবহার করা হয় যেমন : Karman-Pohalhausen রূপান্তর, Croco’s রূপান্তর, Boussenisq রূপান্তর, Von-Mises রূপান্তর।
