Eratosthenes-এর ছাঁকনি ও Euler-এর সোনার চাবি

সংখ্যাতত্ত্বে এবং গোপনীয় বার্তাসঞ্চারের আধুনিক প্রযুক্তিতে মৌলিক সংখ্যার গুরুত্ব অপরিসীম। আজ থেকে 2,300 বছর আগে লেখা Euclid-এর কালজয়ী গ্রন্থ Elements-এ তিনি সহজেই প্রমাণ করেছিলেন যে মৌলিক সংখ্যার শেষ নেই। কোনো একটি মৌলিক সংখ্যাকে সর্বোচ্চ ধরে তিনি দেখান তার চেয়েও বড় একটি মৌলিক সংখ্যা থাকতে বাধ্য। প্রাকৃতিক সংখ্যার অনুক্রমে মৌলিক সংখ্যার আবির্ভাবের কোনো নিয়ম বা প্যাটার্ন খুঁজে পাওয়া যায়নি। গণিতজ্ঞরা এরকম কোনো নিয়মের অনস্তিত্বেরও প্রমাণ দিয়েছেন। গণিতশাস্ত্রে মৌলিক সংখ্যা-সংক্রান্ত গবেষণা এখনো চলেছে। Euclid-এর সমসাময়িক গ্রিক পণ্ডিত Eratosthenes প্রাকৃতিক সংখ্যার অনুক্রমে মৌলিক সংখ্যাগুলিকে চিহ্নিত করার একটি অত্যন্ত সরল পদ্ধতির উল্লেখ করেন। এটি Eratosthenes-এর ছাঁকনি (Eratosthenes sieve) নামে পরিচিত।

প্রথমে বলা দরকার 1859 সাল থেকে সর্বস্বীকৃতভাবে 1 সংখ্যাটিকে আর মৌলিক সংখ্যা হিসেবে ধরা হয় না। সুতরাং মৌলিক সংখ্যা হিসেবে আমরা লিখি – 2, 3, 5, 7, 11, 13, 17, 19, …। 2 ছাড়া আর বাকি সব মৌলিক সংখ্যাই বিজোড়। Eratosthenes-এর ছাঁকনি বোঝার জন্য 2 থেকে শুরু করা যাক। প্রথমে প্রাকৃতিক সংখ্যার অনুক্রম থেকে 2 সংখ্যাটি রেখে 2-এর সব গুণিতকগুলি বাদ দিয়ে দেওয়া হল। ফলে প্রাকৃতিক সংখ্যার অনুক্রম চিত্র 1-এর মত দেখতে হবে। পরের ধাপে 3 সংখ্যাটি রেখে 3–এর সব গুণিতকগুলি বাদ দিয়ে দেওয়া হল। ফলে প্রাকৃতিক সংখ্যার অনুক্রম চিত্র 2-এর মত দেখতে হবে।

তৃতীয় ধাপে 5 সংখ্যাটি রেখে 5–এর সব গুণিতকগুলি বাদ দিয়ে দেওয়া হল। ফলে প্রাকৃতিক সংখ্যার অনুক্রম চিত্র 3-এর মত দেখতে হবে।

চিত্র 1 – 3 দেখলে বোঝা যাবে যে ধাপে ধাপে যৌগিক সংখ্যাগুলি সরিয়ে নেওয়া হচ্ছে। চিত্র 3-এ Eratosthenes-এর ছাঁকনি দিয়ে 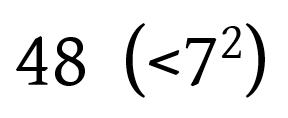পর্যন্ত সব যৌগিক সংখ্যাগুলি গলে গেছে, এবং 2 থেকে 47 পর্যন্ত সব মৌলিক সংখ্যাগুলি ধরা পড়েছে। এইভাবে ধাপে ধাপে এগিয়ে মৌলিক সংখ্যাগুলিকে চিহ্নিত করা যাবে। এই অত্যন্ত আপাত সরল পদ্ধতিটি সংখ্যাতত্ত্বে খুবই উপযোগী হিসেবে গণ্য হয়। গণিতশাস্ত্রের ইতিহাসে অন্যতম মহান গণিতজ্ঞ Leonhard Euler এই পদ্ধতি ব্যবহার করে অন্তহীন প্রাকৃতিক ও মৌলিক সংখ্যাগুলিকে একসূত্রে বাঁধতে সক্ষম হন। যেটি Euler-এর ‘সোনার চাবি’ (Golden Key) হিসেবে অভিহিত। পরে সেখান থেকে গণিত-গবেষণার অনেক গুরুত্বপূর্ণ শাখার সৃষ্টি হয়। এই নিবন্ধে এই বিষয়টি আলোচনা করার আগে আমরা সংক্ষেপে এই কাজগুলির ভূমিকা পর্বটি বিবেচনা করব।

চতুর্দশ শতাব্দীতে বহুবিদ্যাবিশারদ ফরাসি পণ্ডিত Nicolas Oresme প্রমাণ করেন যে নীচে দেওয়া বিপরীত শ্রেণিটি (Harmonic Series)

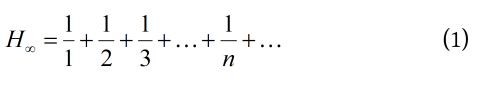
অপসারী (divergent)। এটি প্রমাণ করার জন্য তিনি লেখেন –

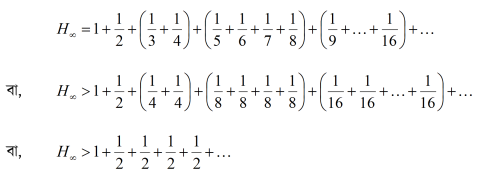
সুতরাং অসীম বিপরীত শ্রেণি অন্তহীন সংখ্যক (1/2)-এর যোগফলের চেয়ে বেশি, অর্থাৎ শ্রেণিটি অপসারী

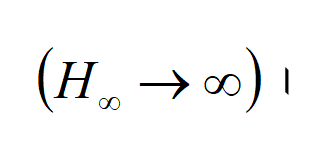
Nicolas Oresme-এর পদ্ধতি অনুসরণ করে আমরা দেখব

শ্রেণিটি অভিসারী। এই সিদ্ধান্তটি প্রমাণ করার জন্য লিখি –

1644 সালে ইতালির গণিতজ্ঞ Mengoli তৎকালীন ইউরোপের বিখ্যাত গণিতজ্ঞদের

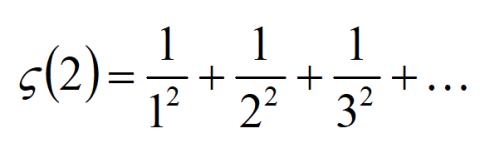শ্রেণিটির মান নির্ণয় করতে অনুরোধ করেন।

1655 সালে Wallis-এর উত্তর দেন “আমি এই মানটি দশমিক বিন্দুর পর তিনটি অঙ্ক সঠিক জানি”।
1689 সালে Jakob Bernoulli বলেন “এই মানটি 2-এর চেয়ে কম। অন্যরা দয়া করে সাহায্য করুন”।
1721 সালে Jakob-এর ভাই Johann এবং তাঁর পুত্র Daniel Bernoulli বলেন “ এটির মান (8/5)-এর কাছাকাছি”।

প্রায় ঐ সময়েই Goldbach-এর উত্তর “মানটি (41/35) = 1.64-এর চেয়ে বেশি, কিন্তু (5/3) = 1.666… -এর চেয়ে কম”। Leibniz ও DeMoivre কোনো উত্তর দেননি। 1735 সালে Euler এই বিখ্যাত (Basel Preoblem নামে খ্যাত) সমস্যার সমাধান করে ইউরোপের শ্রেষ্ঠ গণিতজ্ঞের স্বীকৃতি পান। Bernoulli পরিবার এবং Euler আদতে Basel-এর বাসিন্দা ছিলেন। Euler দেখান, 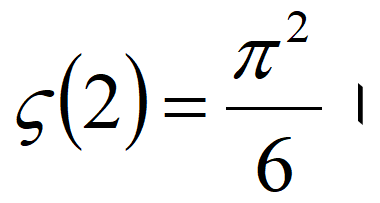সমাধানে জ্যামিতির সর্বজনীন ধ্রুবক 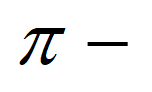এর আবির্ভাব আশ্চর্যজনক বললে কম বলা হয়। যদিও 1735 সালে Euler-এর দেওয়া মানটি সঠিক, কিন্তু তাঁর পদ্ধতিটি গাণিতিকভাবে নিখুঁত ছিল না। তিনি পরে আরও দুটি উন্নততর পদ্ধতি পেশ করেন। তাছাড়া s-এর সকল জোড় মানের জন্য 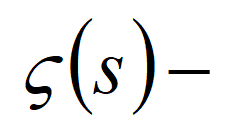এর মান নির্ণয় করে দেখান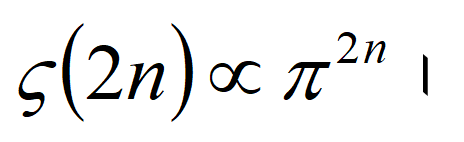

1737 সালে এই 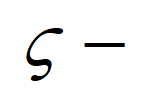অপেক্ষক ব্যবহার করে Euler অন্তহীন প্রাকৃতিক ও মৌলিক সংখ্যাগুলিকে তাঁর ‘সোনার চাবির’ সাহায্যে একসূত্রে গাথেঁন। আমরা সেটি দেখানোর জন্য প্রথমে লিখি –

লক্ষণীয় চিত্র 1-এর মত 2-এর সমস্ত গুণিতক সমীকরণ (5)-এর ডানদিক থেকে সরে গেছে। Eratosthenes-এর ছাঁকনির মত মৌলিক সংখ্যা 2 সমীকরণ (5)-এর বাঁদিকে ধরা পড়েছে। পরের ধাপে সমীকরণ (5)-এর উভয়দিককে 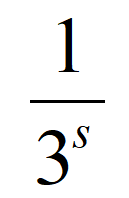দিয়ে গুণ করে পাই –

সমীকরণ (5) থেকে সমীকরণ (6) বিয়োগ করে লিখি –

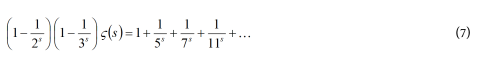
এই প্রক্রিয়া সমানে চালিয়ে শেষে পাওয়া যাবে –

যেখানে n সব প্রাকৃতিক সংখ্যা এবং p সব মৌলিক সংখ্যাগুলিকে নির্দেশ করে। সমীকরণ (8) যেটি সমস্ত প্রাকৃতিক সংখ্যার অনোন্যকের যোগফলের সঙ্গে সমস্ত মৌলিক সংখ্যার অনোন্যক সংক্রান্ত পদগুলির গুণফলকে সম্পর্কিত করে, সেটি গণিতশাস্ত্রে Euler-এর ‘সোনার চাবি’ নামে বিখ্যাত। এই চাবি ব্যবহার করে সংখ্যাতত্ত্বের এবং গণিত জগতের অনেক রহস্যের দ্বার উন্মুক্ত হয়েছে।

Euler-এর 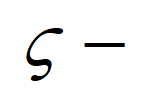অপেক্ষকের চল s-কে Riemann একটি জটিল রাশি 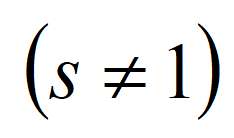দিয়ে প্রকাশ করেন – এবং সেই অপেক্ষকটি এখন Riemann-এর 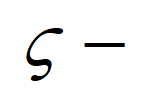অপেক্ষক নামে অভিহিত। 1859 সালে Riemann তাঁর 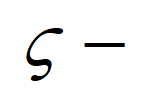অপেক্ষক সম্বন্ধে একটি অনুমানের (গাণিতিক প্রমান ছাড়া) উল্লেখ করেন – যেটি ‘Riemann Hypothesis’ নামে বিখ্যাত। এই অনুমানের কোনো বিপরীত উদাহরণ বা গাণিতিক প্রমাণ আজও অধরা। অনুমানটি সঠিক হলে মৌলিক সংখ্যা-সংক্রান্ত একটি গুরুত্বপূর্ণ প্রশ্নের সন্তোষজনক সমাধান হবে। গত 160 বছরে ‘Riemann Hypothesis’ নিয়ে প্রচুর গবেষণা চলছে – সমাধানকারীর জন্য মূল্যবান আর্থিক পুরস্কারের ঘোষণাও হয়েছে। গণিতজ্ঞরা অনেক সমতুল উপপাদ্যেরও সন্ধান দিয়েছেন। অর্থাৎ সেগুলি প্রমাণিত হলে, ‘Riemann Hypothesis’ সঠিক প্রমাণিত হবে। সেই রকম একটি উপপাদ্য1 বিপরীত শ্রেণি সংক্রান্ত – তাই সেটির উল্লেখ করে নিবন্ধটি শেষ করব।

তথ্যসূচি
1. A. K. Mallik (2020) – Songkhyar Golpo (second edition), Paschimbanga Gonit Parishod, Gobardanga.
2. A. K. Mallik (2018) – Popular Problems and Puzzles in Mathematics, IISc Press, Bengaluru.
3. J. C. Lagairas (2002) – An Elementary Problem Equivalent to The Riemann Hypothesis, American Mathematical Monthly, vol. 109, pp 534 – 543.