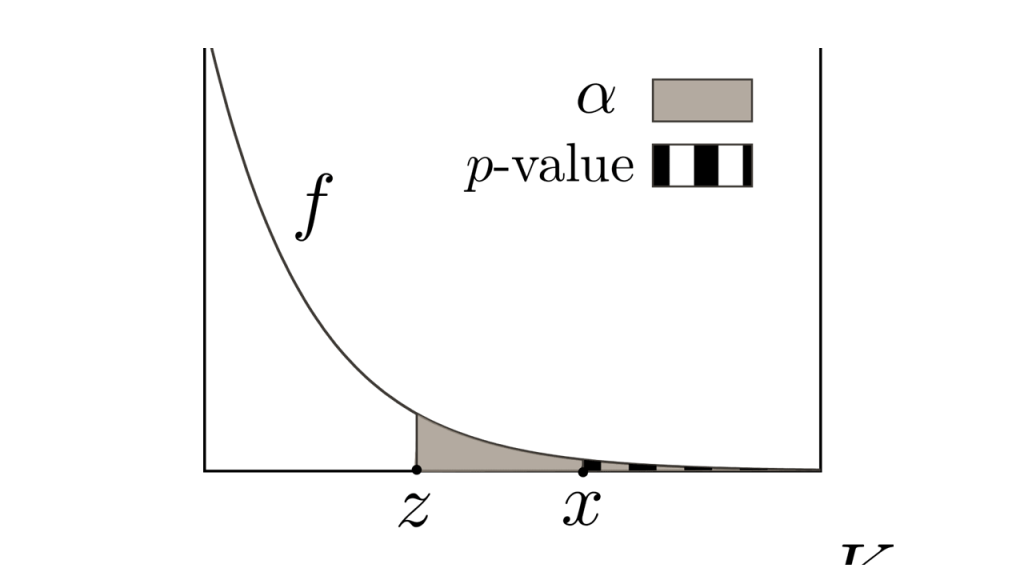
সহজ কোথায় বলতে গেলে, p-value, একটি সংখ্যা, যার দ্বারা কোনও ঘটনা বা পরিস্থিতি ঘটার সম্ভাবনাকে অঙ্কের নিয়মে, বিজ্ঞানসম্মত উপায়ে প্রকাশ করার চেষ্টা করা হয়। সম্ভাবনা বিষয়ক চিন্তাভাবনা অতি প্রাচীন কাল থেকে মানুষের দৈনন্দিন জীবনের সঙ্গে যুক্ত। চিন্তাশীল মানুষের হাতে পরে বিজ্ঞানের জগতে এর অনুপ্রবেশ ঘটে অনেক পরে। মধ্যযুগীয় ইউরোপের ইতিহাস ঘাঁটলে আমরা দেখতে পাই যে রোমান সম্রাজ্যের শেষের দিকে এবং তার পতনের পর সমগ্র সমাজ ও জ্ঞানচর্চা ধর্মগুরুদের দ্বারা নিয়ন্ত্রিত হতে থাকে ফলে বিজ্ঞানচর্চা বিলম্বিত হয়। কিন্তু মানুষের জীবনশৈলীর মধ্যে থেকেই উঠে আসতে থাকে বিজ্ঞানচর্চার উপকরণ। সেই সময়ের জনপ্রিয় বিনোদন ছিল পাশা খেলা। জুয়ারীরা সম্ভাব্য পছন্দের দান পরার ভবিষ্যদ্বাণী নিয়ে মেতে ওঠে আর গাণিতিকরা সেই সম্ভাবনার অংক কষায় নিমগ্ন হয়। শুরু হয় সম্ভাবনা বা probability-র বিজ্ঞানসম্মত চর্চা। এক ফরাসি গনিতপ্রিয় মানুষ, আন্তয়েন গমবল্ড, পাশাখেলার একটি কাল্পনিক সমস্যার উল্লেখ করেন। পাস্কাল ও পিয়ের ফার্মাত নামক সেদেশের দুই গণিত-বিশেষজ্ঞ তা সমাধানের জন্য গাণিতিক পদ্ধতির ব্যবহার করেন। ১৬৫৪ সাল নাগাদ এভাবে জন্ম নেয় সম্ভাবনার ত্বত্ত বা probability theory। ঘটনাক্রমে, বস্তুর ভৌত অবস্থান বা কোনও ঘটনা ঘটার সম্ভাবনা নিয়ে বৈজ্ঞানিক লেখালিখি ও গাণিতিক বিশ্লেষণ ১৭০০ শতাব্দীর সময় থেকে চোখে পরে। ডাক্তার জন আরবুথনট, জন্মসূত্রে স্কটিশ, লণ্ডনের বাসিন্দা, পেশায় চিকিত্সক ও গণিতপ্রেমি, ১৭১০ সালে তার বিখ্যাত পর্যবেক্ষন প্রকাশ করেন। উনি দেখান, লন্ডনে বিগত ৮০ বছর ধরে সদ্যজাত শিশুদের মধ্যে পুরুষ এবং স্ত্রীলিঙ্গের অনুপাত বরাবর একই বজায় থেকেছে। এটি যে কাকতালীয় নয় তা তিনি সম্ভাবনা বা probability-র অঙ্ক কষে উপস্থাপন করেন এবং দূরদর্শী ঈশ্বরের ইচ্ছাতেই এরকম ঘটে চলেছে বলে মত প্রকাশ করেন। ডাক্তার আরবুথনট যাই উপসংহার টেনে থাকুন না কেনো, আমরা পি-ভ্যালু নিয়ে যে গল্প শুরু করেছি তার বীজ ওই লোকটির কাজের মধ্যে নিহিত আছে। পরবর্তীকালে গণিতশাস্ত্রের পাশাপাশি রাশিবিজ্ঞান বিজ্ঞানের স্বতন্ত্র শাখা হিসেবে গড়ে উঠতে থাকে। বার্নৌলি, ল্যাপলাস, কুয়েটলেট, পিয়েরসন ইত্যাদি বিজ্ঞানীদের কাজ রাশিবিজ্ঞানকে সমৃদ্ধ করে। রাশির প্রকৃতি, বিন্যাস, বিস্তার ইত্যাদির বৈজ্ঞানিক পরিভাষা তৈরি হয়। শুরুরদিকে রাশিবিজ্ঞানের ব্যবহার মূলত জোতির্বিজ্ঞান, ভূবিদ্যা ও পদার্থবিদ্যায় সীমাবদ্ধ থাকলেও ক্রমশ সমাজবিদ্যা ও জীববিদ্যার বিভিন্ন শাখায়ও এর প্রয়োগ হতে থাকে। কিন্তু জীবগোষ্ঠীর বিভিন্ন শরীরাবৃত্তিয় ও চারিত্রিক বৈশিষ্ঠের তুলনামূলক পর্যবেক্ষন এবং ‘বৈজ্ঞানিক অনুমানের (Hypothesis)’ সত্যতা যাচাই করা সমাজবিদ্যা ও জীববিদ্যার মূল উপপাদ্য বিষয়, যা অন্যান্য জড়বিজ্ঞানের শাখার গবেষণা পদ্ধতির থেকে খানিকটা আলাদা। তাই এই শাখায় রাশিবিজ্ঞানের ব্যবহারিক পরিবর্তনের প্রযোজনীয়তা দেখা দেয়।
রোনাল্ড ফিশার ১৯২৫ সালে তার সুবিখ্যাত বইটিতে বিভিন্ন শাখার গবেষকদের উপযোগী রাশিবিজ্ঞানের ব্যবহারিক প্রয়োগের উপায় আলোচনা করেন। রোনাল্ড ফিশারের অনেক আগেই তার পূর্বসূরীরা ‘দুটি বৈজ্ঞানিক পর্যবেক্ষণের’ মধ্যেকার তফাত কাকতালীয় কী না বোঝার জন্য রাশিবিজ্ঞানের ব্যবহার শুরু করেন ও ‘পি-ভ্যালু (p-Value)’ নামক গাণিতিক রাশির উদ্ভাবন করেন। ‘বৈজ্ঞানিক অনুমানের (Hypothesis)’ সত্যতা যাচাই করতে প্রথমেই ধরে নেওয়া হয় যে সঠিক প্রমাণ না পাওয়া গেলে এই ‘অনুমান (Hypothesis)’ ভুল। খানিকটা আদালতে অভিযুক্তের বিচারের মতো ব্যাপার। আদালতে ধরে নেওয়া হয় যে অভিযুক্ত নিরপরাধ। তারপর তথ্যপ্রমান ঘেঁটে বিচার করা হয় যে সে অপরাধী কী না। রোনাল্ড ফিশার ও নেইমান-পিয়েরসন জুটি এই ত্বত্তকে আরো পরিশীলিত করে ব্যবহারপযোগী করে তোলেন, ফলে রাশিবিজ্ঞানভিত্তিক তুলনামূলক পদ্ধতি ও পি-ভ্যালু গবেষকদের মধ্যে জনপ্রিয় হয়ে ওঠে। ‘বৈজ্ঞানিক অনুমানের (Hypothesis)’ যুক্তি ও কিছু পূর্বশর্তের উপর নির্ভর করে পি-ভ্যালু (p-Value) ব্যাবহারের দুটি ত্বত্তগত পদ্ধতি, ফিশারীয় (Fisherian) ও নেইমান-পিয়েরসনিয় পদ্ধতি নামে পরিচিতি লাভ করে। রোনাল্ড ফিশার ‘বৈজ্ঞানিক অনুমান (Hypothesis)’ ভ্রান্ত হওয়ার সম্ভাবনকে বিচার করার জন্য পি-ভ্যালুর গাণিতিক মান ০.০৫ নির্দিষ্ট করার প্রস্তাব করেন। সহজ কোথায় এর অর্থ হলো কোনও বৈজ্ঞানিক পরীক্ষা ২০ বার পুনরাবৃত্তি করলে একবার ভ্রান্ত ফলাফল পাওয়ার সম্ভাবনা থাকবে। পি-ভ্যালু যত কম হবে ভ্রান্ত ফল পাওয়ার জন্য আরো বেশি বার বৈজ্ঞানিক পরীক্ষা পুনরাবৃত্তি করতে হবে। আরো সহজে বললে, যত কম পি-ভ্যালু, দুটি বৈজ্ঞানিক পর্যবেক্ষণের মধ্যে গাণিতিক সম্পর্ক ততো জোরালো। এটা বুঝতে গিয়ে একটু সাবধান হতে হবে। রাশিবিজ্ঞানে ‘ভ্রান্ত ফল পাওয়ার সম্ভাবনা (False Discovery rate)’ নামক আরেকটি গননা করা হয়ে থাকে যা এই পি-ভ্যালুর ধারনা থেকে সম্পুর্ন আলাদা। যাইহোক, এভাবে রাশিবিজ্ঞানের জটিল গননা পদ্ধতি অন্যান্য গবেষকদের কাছে অতি সরল ভাবে পরিবেশিত হয়। রাশিবিজ্ঞানের এই পি-ভ্যালু (p-Value) পদ্ধতির ব্যবহার, মূলত, সমাজবিদ্যা ও জীববিদ্যার গবেষকদের পর্যবেক্ষণের গ্রহণযোগ্যতা গবেষণাপত্রে ও বিজ্ঞানমহলে অনেকখানি বাড়িয়ে দেয়। এর প্রভাব আজও ক্রমশ বেড়ে চলেছে। গবেষণাপত্র প্রকাশক সংস্থাগুলিও পি-ভ্যালু (p-Value) পদ্ধতির ব্যবহারে জোর দিতে থাকে। ফলসরূপ, সম্প্রতিককালে দেখা যাচ্ছে প্রায় ৯৬ শতাংশ জীববিজ্ঞান গবেষণাপত্রে পি-ভ্যালু ০.০৫ মানদন্ড ব্যবহার করা হয়েছে।
ফিশার প্রচলিত পি-ভ্যালুর মান ০.০৫ যে একেবারে সকলে মেনে নিয়েছিল তা কিন্তু নয়। এই ধারণার যতেচ্ছ ও ভ্রান্ত ব্যবহার চিন্তার কারণ হয়ে দাঁড়ায়। যেমন পি-ভ্যালু ০.০৫ মানদন্ড অনুযায়ী ‘ভ্রান্ত ফল পাওয়ার সম্ভাবনা (False Discovery rate)’ প্রায় ৩০ শতাংশের কাছাকাছি চলে আসে। আবার গবেষণাপত্র প্রকাশের তাগিদে, বিশেষত আধুনিক কালে, কিছু গবেষক প্রয়োজনীয় পূর্বশর্তগুলি না মেনেই পি-ভ্যালু ০.০৫ মানদন্ড ব্যবহার করতে থাকে। ফলে গুরুত্বহীন পর্যবেক্ষন গুরুত্বপূর্ণ বলে দাবী করার প্রবণতা বাড়তে থাকে। দুটি বৈজ্ঞানিক পর্যবেক্ষণের মধ্যে সংখ্যাগত সম্পর্ক ও কার্যকারণ সম্পর্কের তফাত করা কঠিন হয়ে পরে। বৈজ্ঞানিক পর্যবেক্ষনকে ‘রাশিবিজ্ঞানের নিয়মমাফিক পি-ভ্যালু-নির্ভর গুরুত্বপূর্ণ অথবা গুরুত্বহীন’ এই দুটি ভাগে ভাগ করলে বিজ্ঞানের অনেক সত্য অজানা থেকে যায়। বিজ্ঞানকে ‘হ্যাঁ’ এবং ‘না’ তে ভাগ করতে গিয়ে একটি সাদা-কালো ছবি আমরা দেখি, মাঝের অন্য রঙগুলো নজরে পরেনা। দোষটা রাশিবিজ্ঞান বা পি-ভ্যালুর নয়, বিজ্ঞানের চর্চায় নিযুক্ত ব্যক্তির উদ্দেশ্য ও ইচ্ছাই গুরুত্বপূর্ণ। তাই সম্প্রতিক কালে গবেষক ও বিজ্ঞানকর্মীরা সংখাতত্বের সঠিক ব্যবহার নিয়ে চিন্তাভাবনা করতে শুরু করেছেন। বিজ্ঞানচর্চাকে হতে হবে যুক্তিনির্ভর ও যান্ত্রিকতামুক্ত। অন্ধের মতো একটি সংখ্যার পিছনে দৌড়ে তা কখনও সম্ভব নয়। পি-ভ্যালুর একটি নির্দিষ্ট মানের বদলে ধারাবাহিক মাপকাঠির প্রচলন ও গবেষনার প্রয়োজনীয়তায় এর নির্দিষ্ট মান ০.০৫-এর আরও নিচে নামিয়ে আনার পক্ষপাতি অনেকে। গবেষনার কাঠামো ও পরিকল্পনার উপর ভিত্তি করে পি-ভ্যালুর গুরুত্ত্ব যাচাই করার কথাও উঠে এসেছে। ফিশারীয় (Fisherian) ও নেইমান-পিয়েরসনিয়, এই দুটি ‘ঘনত্ত্ববাদী পদ্ধতির (Frequentist approach)’ বাইরে বেরিয়ে ‘বায়েশীয় (Bayesian) তত্ত্ব’ ব্যাবহারের কথাও বিশেষজ্ঞরা বলছেন। এভাবেই রাশিবিজ্ঞানের সঠিক প্রয়োগ পরিপূর্ণতা লাভের দিকে এগিয়ে চলেছে।
